Heat Engine, Refrigerating Machine and Heat Pump

 

Overview of Heat Engines

IMAGE SOURCE

Definition

A heat engine is a device that converts heat energy into mechanical energy. Heat engines extract energy from burning fuel and convert a fraction of it into mechanical energy.

Operating Principle

All heat engines utilize a working substance that undergoes cooling, heating, compression, expansion, and sometimes a change of phase. Examples include:

• Steam Engine: Water is the working substance.
• Gasoline Engine: The working substance is the gasoline-air mixture.

Characteristics of Heat Engines

Heat engines share the following characteristics:

1. They receive heat from a high-temperature reservoir (heat source).
2. They convert part of this heat into work (usually through a rotating shaft).
3. They reject the remaining waste heat to a low-temperature sink (cold reservoir), e.g., the atmosphere or rivers.
4. They operate on a cyclic process.

Classification of Heat Engines

Heat engines can be classified into two major types:

• Internal Combustion Engine: Burns fuel inside the engine (e.g., Otto engines and diesel engines).
• External Combustion Engine: Burns fuel outside the engine (e.g., steam engine).

Operating Cycle of a Steam Engine

1. Water is pumped to a boiler where it is vaporized to produce steam.
2. The steam is admitted into a cylinder where it expands.
3. The expanding steam pushes a piston, doing work in the process.
4. The spent steam is discharged to a condenser and returned to the boiler. In some engines, the spent steam is discharged to the atmosphere.

 A heat engine  operating in a cycle and producing a net quantity of work from supply of heat can be represented schematically  as shown in the Figure.

 

Fig. Schematic diagram of heat engine that absorbs energy Qh from  the hot reservoir, and expels energy Q c to the cold reservoir, and does wor W.

Thermal Efficiency of Heat Engines

The thermal efficiency $e$ of a heat engine measures how well the engine operates. It is defined as the ratio of work done by the engine to the energy added to the system by heat during one cycle.

Formulas

• Efficiency Equation:

$$e=\left(\frac{W}{Q_h}\right)\times 100$$

• Work Done:

$$W=Q_h-Q_c$$

• Efficiency Expanded:

$$e=\left(\frac{Q_h-Q_c}{Q_h}\right)\times 100=(1-\frac{Q_c}{Q_h})\times 100$$

Where:

• $Q_h$: Heat supplied from the hot reservoir
• $Q_c$: Heat rejected to the cold reservoir
• $W$: Net work done by the engine
• $e$: Thermal efficiency of the heat engine

SAMPLE PROBLEM:

Heat is transferred to the heat engine from furnace at a rate of   80 MW. If the rate of waste rejected to the nearby river is  50 MW,  determine the power output/network and the thermal efficiency of this engine.

     

SAMPLE PROBLEM:

Find the efficiency of a heat engine that absorbs 2000 J of energy from a hot reservoir and exhausts 1,500 J to a cold reservoir.

Heat Transfer Principle

Heat naturally transfers from a high-temperature medium to a low-temperature medium. However, to transfer heat from a low-temperature medium to a high-temperature one, special devices called refrigerators are required.

Refrigerators

• Refrigerators are cyclic devices that operate on a refrigeration cycle.
• The working fluid used in this cycle is known as the refrigerant.
• Refrigerators and air conditioners function as heat pumps, which are essentially heat engines operating in reverse.

Functionality

• A heat engine typically extracts heat from a hot reservoir and converts part of it into work while rejecting the remaining heat to a cold reservoir.
• Conversely, a heat pump (or refrigerator) extracts heat from a cold reservoir (its interior) and expels it to a hot reservoir (its exterior).

Air Conditioners

• Air conditioners are specialized refrigerators where the refrigerated space is a room or building rather than a food compartment.
• For example, a window air-conditioning unit cools a room by absorbing heat from the room air and discharging it to the outside.

Heat Pumps

• Heat pumps have traditionally been used for cooling homes and are increasingly popular for heating as well.
• They operate by absorbing energy $Q_c$ from a cold storage reservoir and expelling energy $Q_h$ to a hot reservoir.

Schematic Representation

A refrigerator or heat pump can be schematically represented as follows:

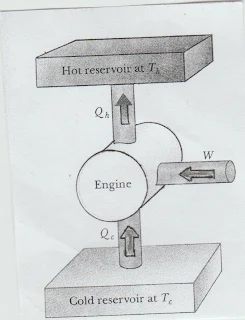Fig.  A heat engine operating in reverse. It is basically the same diagram as that of a heat engine but the arrows have been reversed. 

Work Done:

$$W=Q_h-Q_c$$

Where:

• $Q_c$: Heat absorbed from the cold body
• $Q_h$: Heat rejected to the surroundings
• $W$: Work done or mechanical energy consumed

2. Coefficient of Performance (COP):
   • For Cooling Mode:

$$\text{COP}=\frac{Q_c}{W}=\frac{Q_c}{Q_h-Q_c}$$

• For Heating Mode:

$$\text{COP}=\frac{Q_h}{W}=\frac{Q_h}{Q_h-Q_c}=\frac{T_h}{T_h-T_c}$$

Where:

• $T_h$: Temperature of the hot reservoir
• $T_c$: Temperature of the cold reservoir

Energy Efficiency Ratio (EER)

• The performance of a refrigerating machine is also expressed in terms of the Energy Efficiency Ratio (EER):
  • Thus, $1\text{EER}=3.412\text{COP}$

Typical Values

• Most air conditioners have an EER between 8-12 or a COP of 2.3 to 3.5.
• A unit that removes 1 kWh of heat from a cooled space for each kWh of electricity consumed (COP = 1) will have:
• EER = 3.412

SAMPLE PROBLEM:

How much heat is released by a  refrigerator to the kitchen if in removing 1,000 J of heat from the food inside  it , and it does 500 J of work?

Summary Equation Forms:

• COP (Heating Mode):

$$\text{COP}=\frac{Q_h}{W}=\frac{Q_h}{Q_h-Q_c}=\frac{T_h}{T_h-T_c}$$

• COP (Cooling Mode):

$$\text{COP}=\frac{Q_c}{W}=\frac{Q_c}{Q_h-Q_c}=\frac{T_c}{\left(\frac{T_h}{T_c}\right)}$$

Overview of the Carnot Cycle

Carnot Principle

• The Carnot Principle, named after French engineer Sadi Carnot, states that maximum efficiency is achieved when all processes undergone by the working substance of a heat engine are reversible.

Carnot Heat Engine

• A heat engine operating on the Carnot cycle is referred to as a Carnot heat engine. It is considered an idealized engine that provides the highest possible efficiency between two heat reservoirs.

Processes of the Carnot Cycle

The Carnot power cycle consists of four reversible processes:

1. Isothermal Expansion (Process 1-2):

   • The working substance absorbs heat $Q_h$ from the high-temperature reservoir at a constant temperature $T_h$.
   • The substance expands, and the system does work on the surroundings.

2. Isentropic Expansion (Process 2-3):

   • The working substance continues to expand without heat exchange (adiabatic process), and the temperature decreases as the volume increases.
   • This process is adiabatic and reversible, leading to a reduction in temperature from $T_h$ to $T_c$.

3. Isothermal Compression (Process 3-4):

   • The working substance is compressed at a constant temperature $T_c$, while it rejects heat $Q_c$ to the low-temperature reservoir.
   • The system absorbs work from the surroundings to facilitate compression.

4. Isentropic Compression (Process 4-1):

   • The work is done on the system to compress the working substance further, which raises its temperature without heat transfer.
   • This process is also adiabatic and reversible, bringing the temperature back to $T_h$.

Definitions

• Isentropic Process: An idealized thermodynamic process that is adiabatic, reversible, and involves no transfer of heat or matter. Work transfers are frictionless.

• Isothermal Process: A process in which the temperature remains constant throughout the transition.

Fundamental Equations

1. Work Done:

$$W=Q_H-Q_L$$

Where:

• $Q_H$: Heat added by the hot body (heat input)
• $Q_L$: Heat rejected to the cold body (heat output)
• $W$: Work done by the engine

2. Thermal Efficiency ($e$):
   • The thermal efficiency of a heat engine is defined as the ratio of work done to the heat input:

$$e=\frac{W}{Q_H}$$

• This can also be expressed in terms of temperatures:

$$e=\frac{T_H-T_L}{T_H}\times 100$$

Where:

• $T_H$: Temperature of the heat source (in Kelvin)
• $T_L$: Temperature of the heat sink (in Kelvin)

Definitions

• $Q_H$: The heat added to the system from the hot reservoir.
• $Q_L$: The heat rejected from the system to the cold reservoir.
• $W$: The net work done by the engine.
• $e$: The thermal efficiency of the heat engine, expressed as a percentage.
• $T_H$: The absolute temperature of the heat source.
• $T_L$: The absolute temperature of the heat sink.

SAMPLE PROBLEM:

A  Carnot engine receives 500 kJ heat per cycle from a high temperature source at  652 oC and rejects heat to low temperature sink at 30 0C. Determine the thermal efficiency of this Carnot engine.

Overview of the Reversed Carnot Cycle

Introduction

The Reversed Carnot Cycle is derived from the Carnot heat engine cycle, which is completely reversible. In this reversed cycle, the directions of heat and work interactions are reversed, enabling it to function as a refrigeration cycle.

Operation of the Reversed Carnot Cycle

The reversed Carnot cycle operates in a counterclockwise direction and consists of the following processes:

1. Isentropic Compression (Process 1-2):

   • The working substance (refrigerant) is compressed adiabatically, resulting in an increase in pressure and temperature without any heat transfer.

2. Isothermal Heat Rejection (Process 2-3):

   • The refrigerant rejects heat $Q_H$ to the hot reservoir while remaining at a constant temperature $T_H$.

3. Isentropic Expansion (Process 3-4):

   • The refrigerant expands adiabatically, causing a drop in temperature and pressure while doing work on the surroundings in a frictionless manner.

4. Isothermal Heat Absorption (Process 4-1):

   • The refrigerant absorbs heat $Q_L$ from the cold reservoir while remaining at a constant temperature $T_L$.

Key Equations

1. Work Done:

$$W=Q_H-Q_L$$

Where:

• $Q_H$: Heat rejected to the hot body.
• $Q_L$: Heat absorbed from the cold body.
• $W$: Work done by the refrigerating device.

2. Coefficient of Performance (COP):
   • The performance of a refrigerating machine is quantified by the Coefficient of Performance:

$$COP=\frac{Q_L}{W}$$

• Alternatively, expressed in terms of temperatures:

$$COP=\frac{T_L}{T_H-T_L}$$

Where:

• $T_L$: Temperature of the refrigeration (cold) reservoir.
• $T_H$: Temperature of the heat rejection (hot) reservoir.

Definitions

• QL: Heat absorbed from the cold body (in the refrigeration cycle).
• QH: Heat rejected to the hot body (surroundings).
• W: Work done on the refrigerating system.
• TL: Refrigeration temperature (temperature at the cold reservoir).
• TH: Temperature of heat rejection to the surroundings (temperature at the hot reservoir).

SAMPLE PROBLEM:

A refrigeration system operates on the reversed Carnot cycle. The minimum and maximum temperature are -25 °C  and 72 °C , respectively . If the  heat rejected at the condenser is 6oookJ/min, determine,

a) COP

b)heat absorbed from the cold body;

c) work done by the system; and

d) tons of refrigerant developed 

Selection of Operating Temperatures in Refrigeration Systems

Overview

The selection of operating temperatures in refrigeration systems is crucial and depends on the specific application. The refrigerant temperature must be adequately lower than the ambient or space temperature it is meant to cool in order to effectively absorb heat.

Example: Summer Air Conditioning System

• For a typical summer air-conditioning system, consider a scenario where:
  • The room is maintained at an indoor temperature of 25°C.
  • To offset the heat entering the room, the air must be supplied at a lower temperature of 15°C.

Key Considerations:

• The air conditioner needs to cool the room air from 25°C to 15°C and then recirculate it back into the room.
• To absorb heat effectively, the refrigerant temperature ($t_o$) must be less than 15°C.
• If the temperature difference between the refrigerant and air were zero, the area required for heat exchange would be infinite.

Recommended Refrigerant Temperatures:

• For effective air conditioning in summer, the refrigerant temperature ($t_o$) is generally set around 0°C to 10°C, often used as 5°C.

Refrigeration Temperature Requirements for Common Applications

No.	Application	Refrigeration Temperature ($t_o$, °C)
1	Air conditioning in summer	0 – 10
2	Cold storage	-10 to 2
3	Domestic refrigerator	-25
4	Frozen foods	-35
5	Freeze drying	-35 to -45

The selection of operating temperatures in refrigeration systems is essential for optimizing efficiency and performance. Each application has specific temperature requirements to ensure effective heat absorption and maintain desired conditions.

READ MORE ON : AREA 3 (AB STRUCTURES & ENVIRONMENT ENGINEERING & BIOPROCESS ENGINEERING &  ALLIED SUBJECTS)